Edcite allows collaborative creation of digital assessments similar to SBAC/PARCC
Edcite allows collaborative creation of digital assessments similar to SBAC/PARCC Many assessments that we as teachers have grown accustomed to have noticeable flaws in design including their inability to target what is important in math curriculum, as well as being oversimplified for grading purposes only to leave students guessing, literally, when it comes to their test. Additionally, assessments are often too infrequently used and are simply snapshots of performance whose value is blown way out of proportion, giving us neither an accurate picture of the student's understanding or an accurate measure of their success. That's why no one likes tests, these flaws have to be corrected.
If our goal is to shift our practice to meet the definition of a rigorous math class defined by CCSS as "pursuing conceptual understanding, procedural skill and fluency and application with equal intensity", then our assessments must reflect this shift. Might I suggest innovative ways, fit for the math revolutionary, that we can use in both formative assessments for students' learning and summative assessments of students' learning in each of these three domains of rigor.
1. Summative assessments should give an Accurate Picture of Student Understanding
Nothing surprised me more when I started teaching than the number of high stakes, no retakes allowed assessments that were multiple choice. Not only is making a one time test worth so much absurd, but then you are going to give the student a 25% chance of getting it right by guessing? Some math students, especially the ones who struggle are going to choose that 25% chance often since that doesn't require work or taking the time to know what you are doing. These types of tests are clearly not an accurate picture of students' understanding. I would suggest that tests should neither be a one take, make or break, or multiple choice. Both of these things skew results based on factors you don't want to assess such as how a student is feeling on a given day, how luckily they have guessed, and how much stress plays into their performance. It doesn't matter on which day you show me you have mastered the material, just that you have mastered it. So allowing a retake of a different version of an assessment should be common practice. If I had failed my Praxis exam then I would just take it again, no big deal, just extra time and extra studying. It also doesn't help when students appear to know what they are doing by guessing very well on parts they didn't know. The problem most teachers have with unlimited retakes is that they need to keep regrading materials and creating 50 versions of a test so that students don't see the same one over and over. Technology really comes in handy here, in creating several versions of a test and having it automatically score procedural skill items, that today can go well beyond simple multiple choice questions on a scantron.
I find that the SBAC and PARCC offer models of what collectively created, well designed assessments look like. Despite being a one time, high stakes test, they do a better job than any previous standardized test of eliminating the guesswork of students. They are not perfect of course but they assess all aspects of rigor as I look at the procedural skill and fluency questions that are auto scored and in particular the SBAC's performance task which incorporates conceptual understanding and applications of math. I have found some great tools that help teachers to create similar high quality assessments. My favorite assessment creation tool is Edcite. It allows you to create SBAC/PARCC Style questions that are automatically scored. You can collectively create them with other teachers, share assessments and view data by question, standard, etc. Here is a link to a sample assessment showing several intriguing item types.
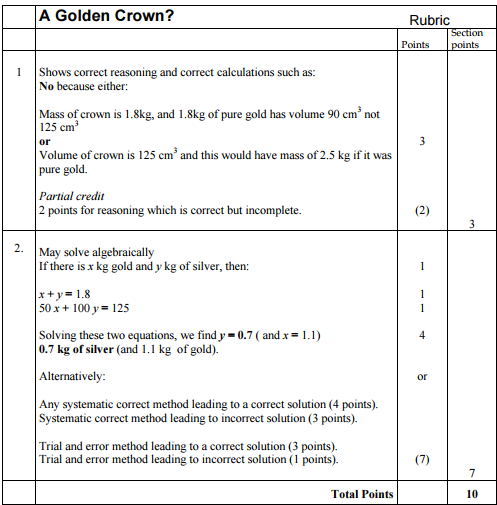
When it comes to performance tasks and summative assessments to demonstrate ability to apply math and display conceptual understanding, I love the full package of materials provided by the Math Assessment Project. They have created summative tasks that assess students conceptual understanding, ability to find patterns and reason mathematically, model with mathematics and apply math to a context. The also come with a rubric that is clear, concise, and common for all users, which makes the data gathered from these reliable and usable. At the last district I worked at I organized the use of these tasks across the district and then math teachers got together for a day of scoring to ensure the grading and use of the rubric was calibrated, collective, and correct. I wonder if we have any reliable data at all that shows that our work with 3 act math and other such activities has truly been helpful in increasing student capacity to problem solve, use applications of math, and conceptually understand topics more completely? I believe that 3 act math is helpful in this regard, but is that just my opinion because my classes seem more engaged? Wouldn't it be nice if we had that collective data curated by unbiased summative tasks that required such skills? I believe these professionally made tasks and rubrics can provide such data. We started to study this in my district on a small scale. See below the images of a simple task and rubric.
After reading an incredible article by Daniel Schneider about assessments and standards based grading, I found myself nodding in agreement with almost all he said. All excepting one point he seemed to find troubling, as I do, that grading is subjective. I get why he says this and in many cases he is right. Teachers do tend to decide, in many cases on their own, what is valuable and what is not, what deserves credit or half credit and what does not, or what is ultimately the correct method and which is not. This shouldn't be as common a practice as it is. I wouldn't want any one person deciding if my work was valuable, it seems inherently biased and unfair. Its one reason why I have heard students brush off their failures in math as the fault of a teacher who doesn't like them.
The way summative assessments should be created is by a collective of teachers, preferably by your professional learning community or other trustworthy group. Point value, which questions need to be asked, what answers deserve credit should all be decided in a council of math teachers. There is safety in such a group decision. It is not math according to Cory Henwood, but more closely approaches the common high standards of mathematics we are all seeking. If we start here we can establish well made, clearly defined rubrics and procedural skill questions that are automatically scored. This takes the bias out of scoring, allows the data gathered by a group of math teachers to be reliable, and in the end saves the teacher time and the heartache of being the arbiter and gatekeeper of math success. Let the students show you what they know on summative assessments. If the assessment policy is set up correctly, allowing retakes, and they are designed to assess what is important, then you will be able to maintain the integrity of your class as well as the most valuable part of your gradebook, and feel good about it.
3. Formative Assessment is Best when it includes Feedback and Discussion
Feedback is the essential aspect to formative assessment. Without feedback as to whether you are on the right or wrong track, a student may continue painfully doing all the wrong things. Formative assessment is one of the most effective practices in education to improving student achievement. If you haven't read "Inside the Black Box" then I invite you to consider it here. The best structure for formative assessment that I have seen when it comes to conceptual development and applications of math, have been created by the Math Assessment Project. An outline of their classroom challenges for formative assessment can be found here, while a listing of all the challenges by category of Problem solving applications or Conceptual development lessons are found here. These lessons are so well outlined with all the materials needed, ideas for feedback, sample student work and connections for discussion and so on, that it makes the process of developing the skills of application in problem solving and deep understanding of concepts attainable, when I might have otherwise given up. Below are some images of some of the lessons. These activities could easily become digital. If the interest is there this may be my next project.
| |
I agree entirely with the premise of Dan Meyer's article, "When Delayed Feedback is Superior to Immediate Feedback". Delaying feedback is important because it can enhance the productive struggle students go through, which increases their desire to know how and why math works. When this desire is increased the likelihood that this engagement lasts and this understanding is retained goes way up. Similar to watching a good TV series, you are hooked and want to know how it ends as you ride the ups and downs of the plot. However, if you were to read the spoilers early in the series, you would feel disenfranchised and not really care about how the series gets to it's eventual ending. Similar to recording a sporting event and finding out the score before you watch it. However, without these spoilers as the plot thickens and the game gets close to an end, you are so engaged and are waiting for the big reveal and its memorable. Although I am not suggesting you will always have that kind of reaction in your math classes, that's what we are shooting for. Too often we cut off their thinking to cut to the chase. How many times has a student asked for help and your immediate reaction is to grab the pencil from their hands to show them? What is that teaching them really? To depend on the teacher when their stuck? Don't worry I am guilty of this.
It's difficult for teachers to implement this delayed feedback, as exemplified by the pencil taking mentioned earlier, and the seeming impatience of every one of our students wanting immediate feedback. Making patient problem solvers is difficult and takes planning and structure. Three act math helps to build this, and the feedback during this process can be enhanced as we use technology to collaborate and discuss student's work. I do this using Nearpod as student's can see others' work after they have submitted their own, when the teacher decides after adequate time to shares it out. To see how this works view this video The classroom challenges mentioned earlier provide this type of structure in productive struggle, teacher feedback and collaboration. The image below depicts a task given at the beginning of the distance time classroom challenge. It has students complete this task individually in silence for 15 mins. The instructor takes these home and gives feedback, some ideas for this are given in the lesson, as well as admonishing not to give scores or grades. This feedback is limited and delayed, it is scaffolding thinking, leading with thoughtful questions and remarks, not giving them answers.
| The next day students will read remarks such as, "How can you figure out Tom’s speed in each section of the journey?" or "What is the total distance Tom covers? Is this realistic for the time taken? Why?/Why not?" Students read the feedback, instead of just looking for a grade and tossing it aside. Afterwards they will partake in some of the collaborative comparison activities like the card sort shown above. Finally, they will have a chance to revisit the task they started individually the day prior. This cycle is powerful, tested, and an easy plug and play into any classroom looking for innovative formative assessment and a method for giving feedback to students in a way that promotes productive struggle and patient problem solving as well as deep conceptual understanding. |
Please help me by sharing your insights here and helping me to promote innovation in assessment.